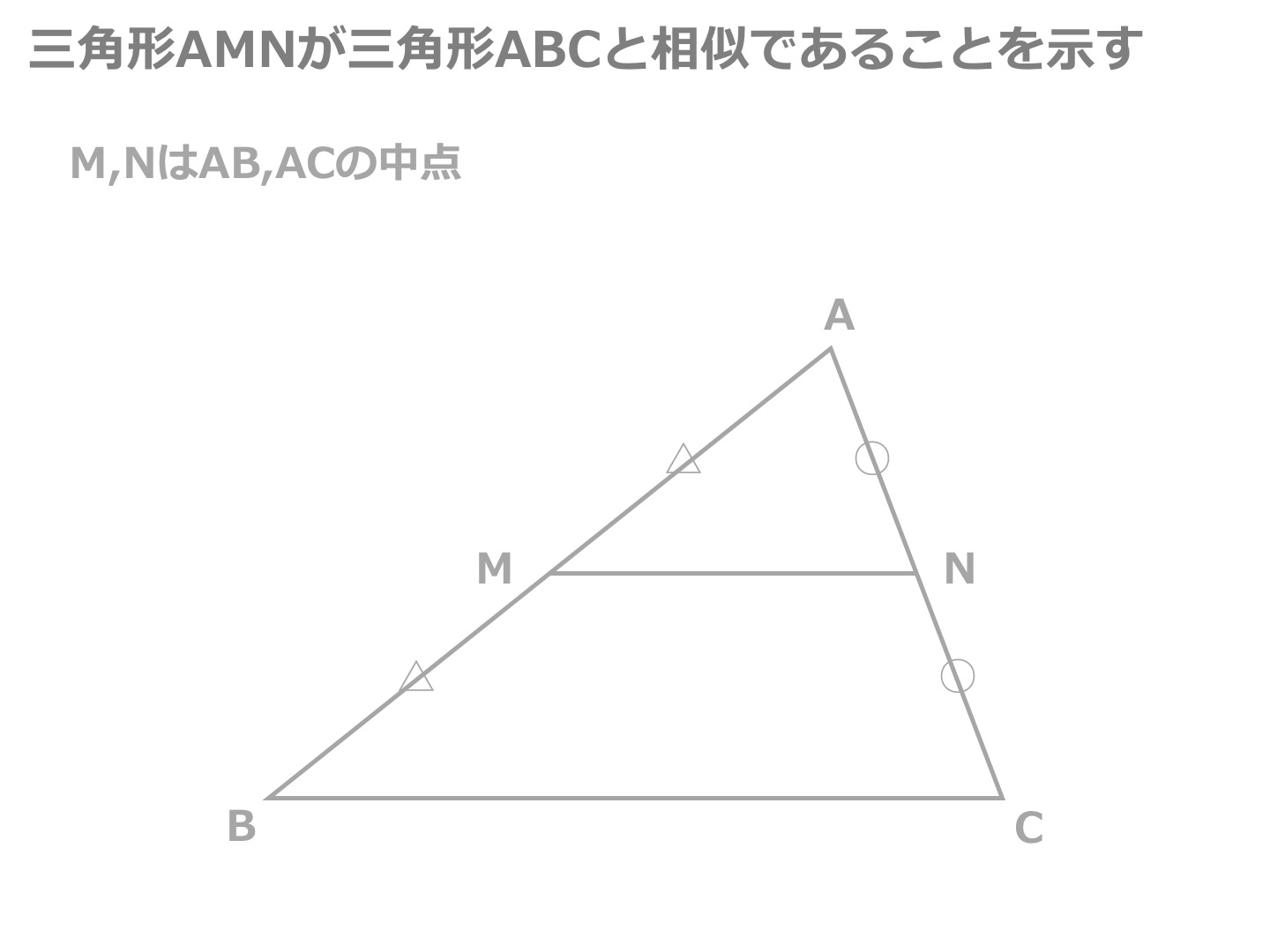
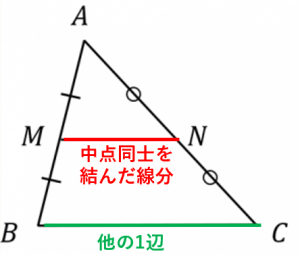
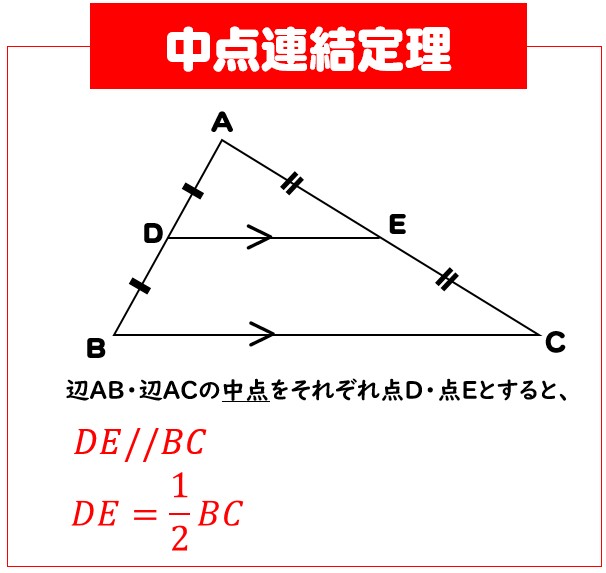
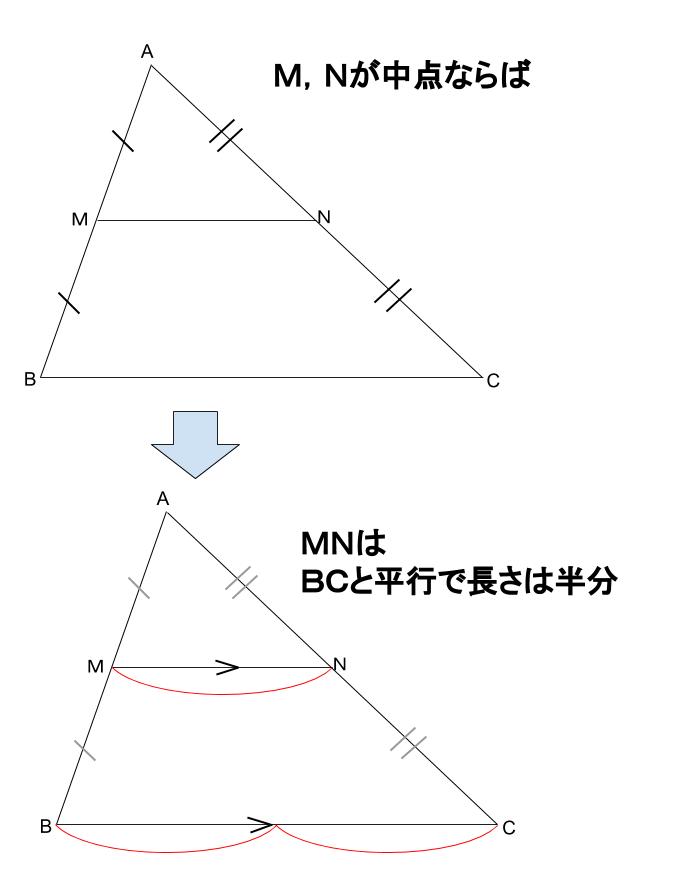
ということができる。 中点連結定理(まとめ) 三角形の 2辺 の中点を結ぶ線分は、残りの辺に平行で、長 さはその半分である。 AM=MB AN=NC ならば MN//BC三角形と線分の比/平行線にはさまれた線分の比/平行線と線分比応用/ 三角形の角の二等分線と線分の比 /中点連結定理:証明問題/長さ・角度の計算/全般/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)

メネラウスの定理が5分でわかる 証明や使い方をイラスト入りで詳しく解説
三角形と比の定理 証明
三角形と比の定理 証明- ナポレオンの定理 任意の ABCに対し、各辺を1辺とした正三角形を外部に作る。 それらの正三角形の重心をそれぞれ結んでできる三角形は正三角形となる。 ピタゴラスの定理の証明で出てくる「花嫁の椅子」を想起させる図ですね。 各正三角形の重心をこの定理には数百通りもの異なる証明があり、例えば、「以下では頂点 a, b, c からなる三角形を abc と表す」「各辺 ab, bc, ca に向かい合う角をそれぞれ ∠c, ∠a, ∠b と表し、各頂点 a, b, c の対辺 bc, ca, ab の長さをそれぞれ a, b, c と表す」「頂点の記号は直角




中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
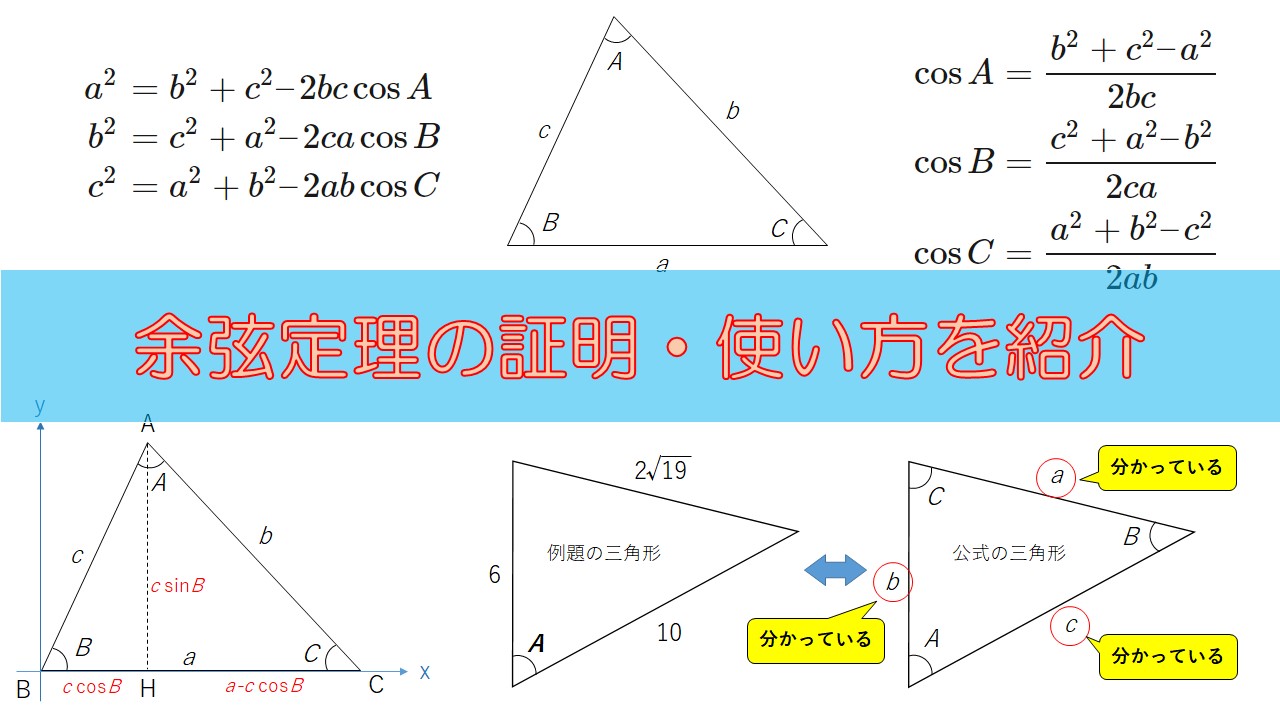
①、②、③より、三角形の相似条件の、 2組の辺の比とその間の角がそれぞれ等しいが使えるから、 ade∽ abc になるね。 これで相似の証明はできた! step2 相似比を求める 三角形の相似比を求めてみよう。 ①のadab=12より、 adeと abcの相似比は1:2になるよ。 まとめ 余弦定理とは、三角形の長さや角度を求めるための公式 求めたいのが長さか角度かによって、2パターンの余弦定理を使い分ける必要がある 余弦定理がなぜ成り立つかを図を使って丁寧に証明した 練習問題を解いて余弦定理に慣れていこう この 三平方の定理には数百もの証明方法があります。今回は相似を利用した基本的な証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理
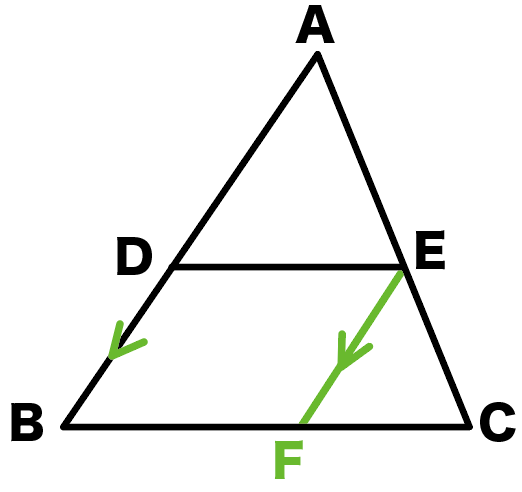
メネラウスの定理 メネラウスの定理とは,三角形と,その頂点を通らないひとつの直線があるときに成り立つ線分の比に関する定理です.証明は平行線と比の定理を $2$ 回用いることに三角形と比 三角形と比 三角形の一辺に平行な直線をひいた時にできる線分の比 について考えていこう。 辺AB を 4等分 するように 点D、E、F をおいてある。 直線は 3点 から 辺BC に平行になるようひいてあるよ。 AD:DE:EF:FB=1:1:1:1 となっている 4.さいごに さて今回はモーリーの定理を三角比を使って 割とゴリゴリの計算 で証明してきました。 証明の中でも何度か現れましたが「同様に」とか「 と を入れ替えれてもいい」といった議論がありました。 これは三角形の持つ「 対称性 」というもの
検索語:三角比 三角関数の加法定理 三角比の三角形への応用 オイラー線の傾き 1 はじめに 高校数学「数学i」において三角比および三 角形などへの応用について学習する。応用の内 容は大体,正弦定理,余弦定理,三角形の解法,では、この法則を使って上の定理を証明していこうと思う。 図2 定理1 図3のような緑の三角形を考える。 \( \angle A\)の二等分線とその二等分線が辺BCと交わる点Pとする。 定理1を証明するためには、 AB AC = BP PC を証明すれば良い。三角形 の 比 の 定理 二等辺三角形とは?定義・定理・性質や、辺の長さ・角度・面積・比の求め方、証明問題などを徹底解説! この記事では、二等辺



平行線と線分の比




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学
三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnと三角比を攻略するには、sin cos tan の計算や正弦定理、余弦定理を完璧にしないといけません。 逆に言うと、 sin cos tan の計算と正弦定理、余弦定理を理解しておけば、三角比では、9割~満点近く目以上から,一般の球面三角形の三角法を導けます.平面三角比と同様,「ピタゴラスの定理」 と「cosine 公式」を使います.頂点C から直線AB に下ろした垂線の足をH, 垂線の長さ をh,AH '=c とします. ACH と BCH でピタゴラスの定理より, cos cos ·cos cos cos( )·cos




中3数学 中点連結定理を使う証明 例題編 映像授業のtry It トライイット



1
三角比の重要公式とその証明を解説します。 今回解説するのは以下の3つの式です。 三角比相互関係の公式! \sin^2 θ\cos^2 θ=1・・・ (1) 物理や数学でよく出てくる 特に重要な公式 を選んだので、最後まで読んで理解してもらえたらと思います!上の正弦定理・余弦定理が必要なので、始めにそれらを導こう。 授業では、余弦定理の証明のみを行います。正弦定理についてはテ キストの最後に参考として証明を載せてあります。 単位球(=半径1の球)面上の三角形について次が成り立つ。1.三角形と比の定理の逆を次のように証明した。空欄をうめなさい。 A <仮定> AD:AB=AE:AC <結論> DE//BC <証明> 2.三角形と比についての定理の逆




初等幾何学から4 中点連結定理 身勝手な主張



1
まず、三角形dbiと三角形dcgに注目します。 共通の角なため∠bdi=∠cdg・・・ⅱ また、ⅰより、∠bid=∠cgd=90°・・・ⅲ ⅱ、ⅲより2組の角がそれぞれ等しいため、三角形dbi∽三角形dcg よって、\(bdcd=bicg\)・・・ⅳ;中点連結定理とは、要は「相似比が1:2の三角形」と理解すればいいです。 三角形の中点を結ぶことによって、相似の三角形を作ることができ、相似比が1:2になるというわけです。 辺の中点なので、相似比が1:2になることは容易に理解できます。 この 二項係数nCrの等式とパスカルの三角形 次のような規則で数を配置したものをパスカルの三角形という \\ 2zh 最上段と両端は1で,\ \textbf {\textcolor {red} {各位置の数は右上の数と左上の数の和}}である \\ これの最も重要な性質は,\ $\bm {\textcolor {red} { (xy)^n\,の
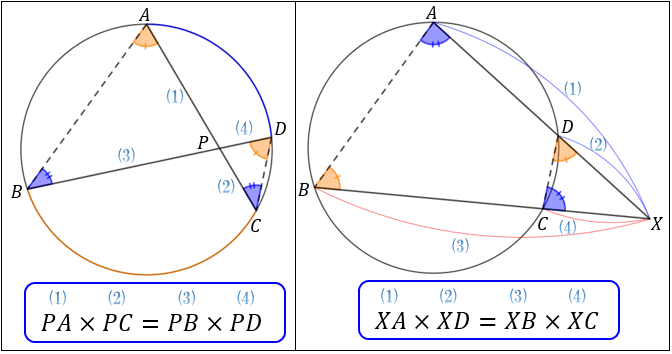



方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b abc が鈍角三角形のときも、同様に証明できます。興味のある人は挑戦してみましょう。 まとめ 正弦定理・余弦定理の内容とそれらを用いた代表的な問題の解き方を説明しました。 正弦定理と余弦定理は、「図形と計量」の分野における基本中の基本です。 三角形の角の二等分線の性質の証明がわかる5ステップ ゆうき先生 三角形の二等分線の定理の証明は、 補助線をひく 相似な図形をみつける 辺の比に注目する 二等辺三角形をさがす 証明をかく の5ステップだよ。




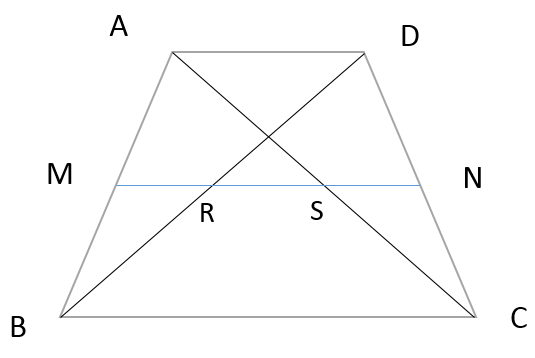
台形と中点連結定理 Ad の台形の辺abと辺cdの中点をe Fとす Okwave




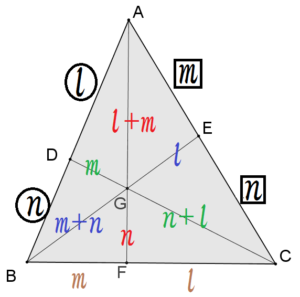
数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
それぞれ、底辺比に置き換えると、 (AF/BF)(BD/CD)(CE/AE)=1 となり、チェバの定理(拡張形)が証明された。 証明2(点Gが三角形の内角の対頂角の範囲内にあるとき) 辺の比を、三角形の面積比で表すと、 AF/BF= ACG/ BCG 角の二等分線とは? 定理や比の性質、証明、問題、作図方法 21年2月19日 この記事では、「角の二等分線」の定理や性質をついてわかりやすく解説をしていきます。 また、定理の証明や作図方法、問題の解き方も紹介していくので、ぜひこの記事を通し 三平方の定理の逆とは、3辺の長さがa、b、cである三角形において、 a²b²=c² が成り立つならば、その三角形は辺cを斜辺とする直角三角形である というものです。 これは図形の証明問題などによく出てくるので頭に入れておきましょう。




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su
チェバの定理というのは、面積比と線分比の考え方の一部、ということなんじゃ トンちゃん なるほどです! といっても具体的に解説しないと、何言ってるかわかりにくいじゃろうから、 さっそく、具体的に解説をしていくかのぉ 目次 1 数学面積三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。 以上が、三角比の相互関係とその証明でした。 証明も合わせて覚えておくと、覚え間違いを無くせます。 90º θ, 180º θ, 90º θ の三角比 では続いて、90º θ や 180º θ の三角比の公式を見ていきます。 まずは公式を一通りご紹介しますね。 <90º θ>



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



1
三角形の五心⑤ 三角形の傍心とその存在証明 スポンサーリンク 高校数学A 平面図形 検索用コード 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\ 2zh その交点を傍心は {1辺と他の2辺の延長からの距離が等しい点正弦定理 三角形の各辺 a , b , c と各角 A , B , C の間に以下に示す関係がある. a sinA = b sinB = c sinC a sin A = b sin B = c sin C この関係を, 正弦定理 という. 三角形の 外接円 の半径を R R とすると, 正弦定理 は, a sinA = b sinB = c sinC = 2R a sin A = b sin B = c sin C = 2A^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた



中点連結定理 問題 On Vimeo




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
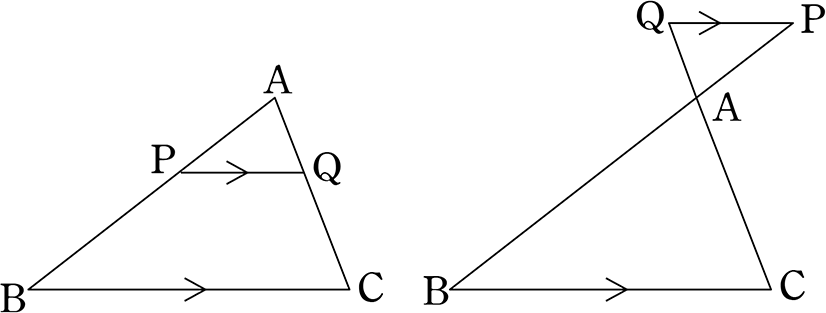



中学数学 図形の相似



中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su



3分でわかる 中点連結定理の証明 問題の解き方をわかりやすく 合格サプリ



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



三角形と比




数学a 図形の性質 以下の問題の解説赤線部について 相似条件は 3辺が等しい Clear




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中3 三角形と比の定理の逆 中学生 数学のノート Clear




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
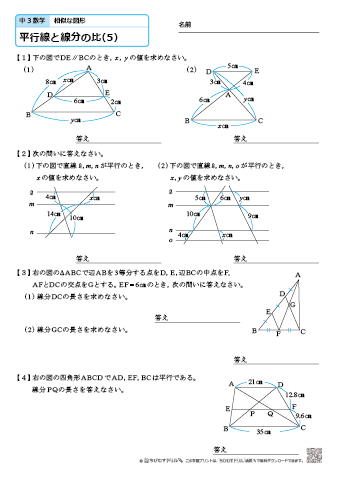



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




この三角形と比の定理というのは Adcと Edbが相似であるから使えるものですか Clear




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学




平面幾何 怜悧玲瓏 高校数学を天空から俯瞰する




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学



三角形と比の定理の逆の証明です Df Acとなるように補助線 Yahoo 知恵袋




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




内角の二等分線 外角の二等分線の比の定理 証明 Youtube




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月




初等幾何学から4 中点連結定理 身勝手な主張
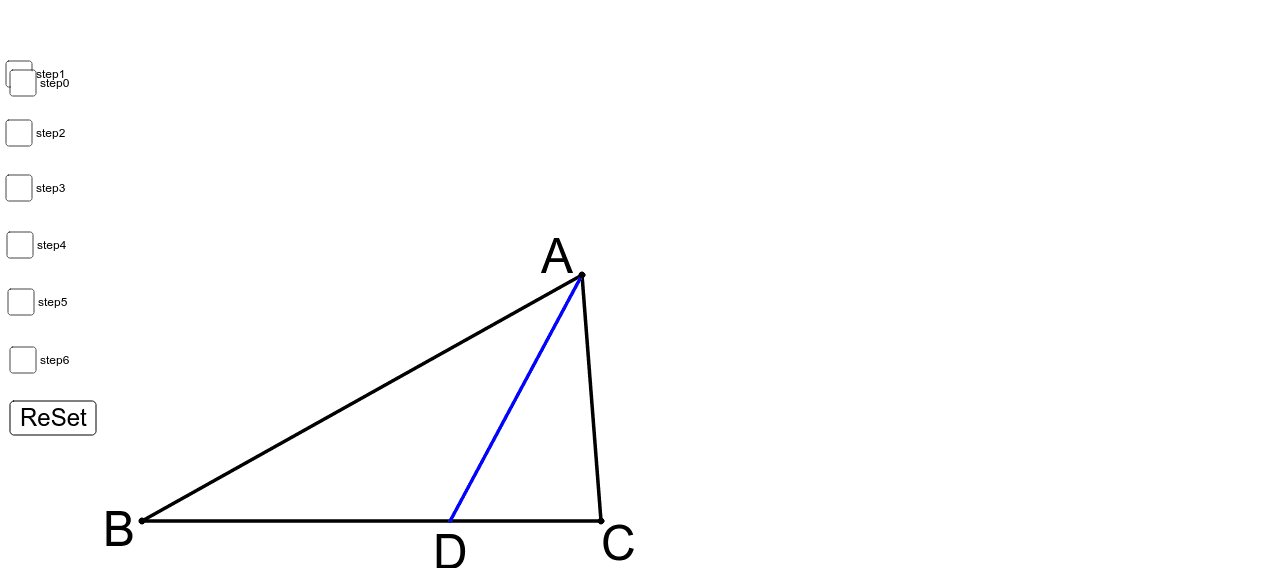



三角形と比の定理の証明1 Geogebra




中点連結定理 無料で使える中学学習プリント
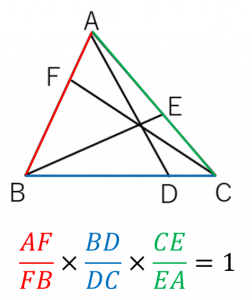



チェバの定理の覚え方 例題 証明 逆 具体例で学ぶ数学




中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
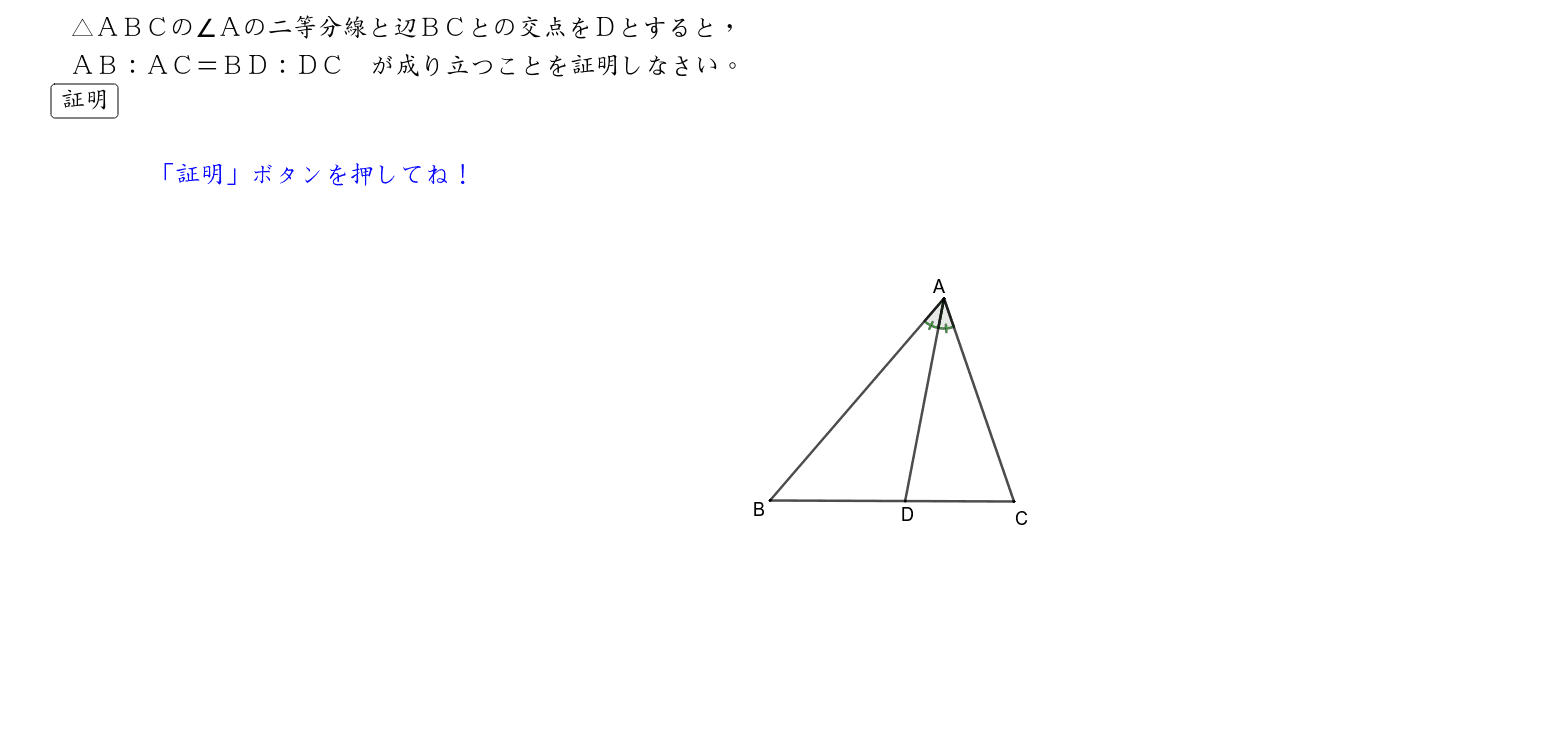



三角形の角の二等分線と比の定理 Geogebra




余弦定理 は三平方の定理の進化版 余弦定理は2つある
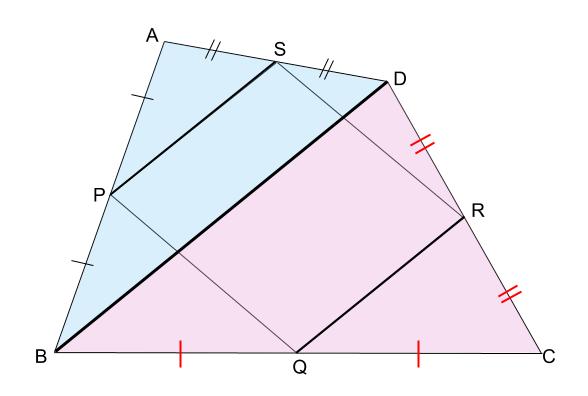



中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su



三角形の角の二等分線定理 外角
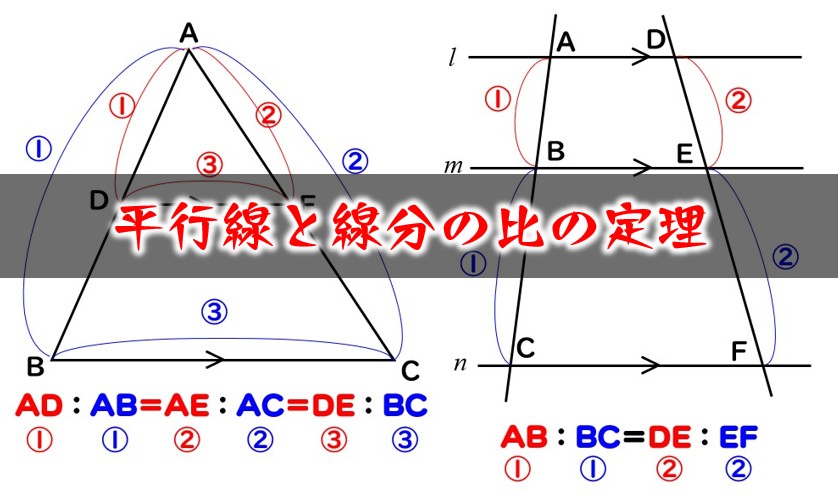



平行線と線分の比の定理 の問題の解き方 数学fun



中点連結定理とその逆の証明および例題 具体例で学ぶ数学
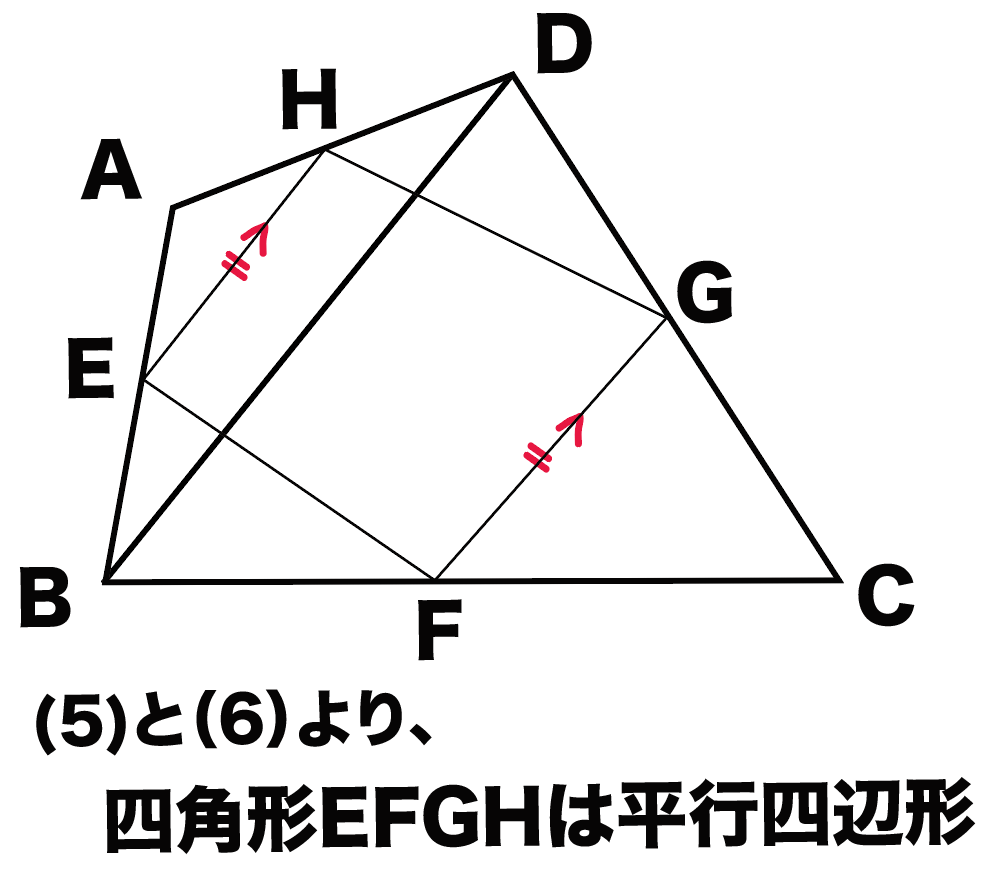



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ




中学数学3 中点連結定理の証明 中学数学 By となりがトトロ マナペディア



中点連結定理 平行四辺形の証明問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




Tossランド 中点連結定理




中3数学 中点連結定理を使う証明 練習編 映像授業のtry It トライイット



Studydoctor三角形と平行線の比の証明 中3数学 Studydoctor
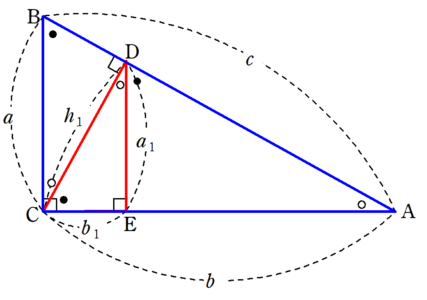



三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも




メネラウスの定理が5分でわかる 証明や使い方をイラスト入りで詳しく解説



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典



中学数学 図形の相似



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中点連結定理とは 三角形の問題で使い方をマスターしよう 中学や高校の数学の計算問題



中学数学 中点連結定理 三角形 四角形 台形 偏差値40プログラマー




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



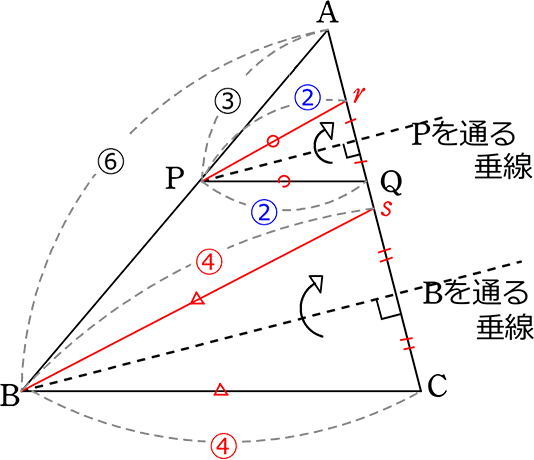
対線比の定理 Fukusukeの数学めも
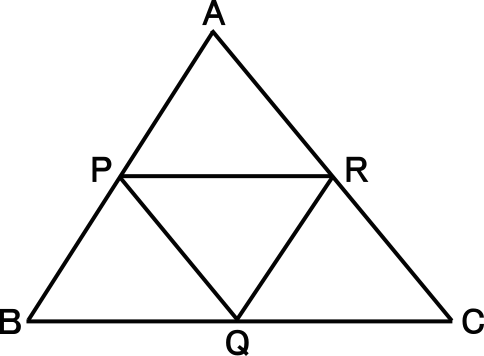



中学3年数学練習問題 中点連結定理 図形と相似



中点連結定理とは 証明 問題の解き方の解説 数学fun



三角形と比



高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト



おもしろ数学講座



1角共有の三角形の面積比 まなびの学園




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




中点連結定理とは 証明 問題の解き方の解説 数学fun




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear




中点連結定理を即理解 周囲と差をつける秘訣とは 高校生向け受験応援メディア 受験のミカタ
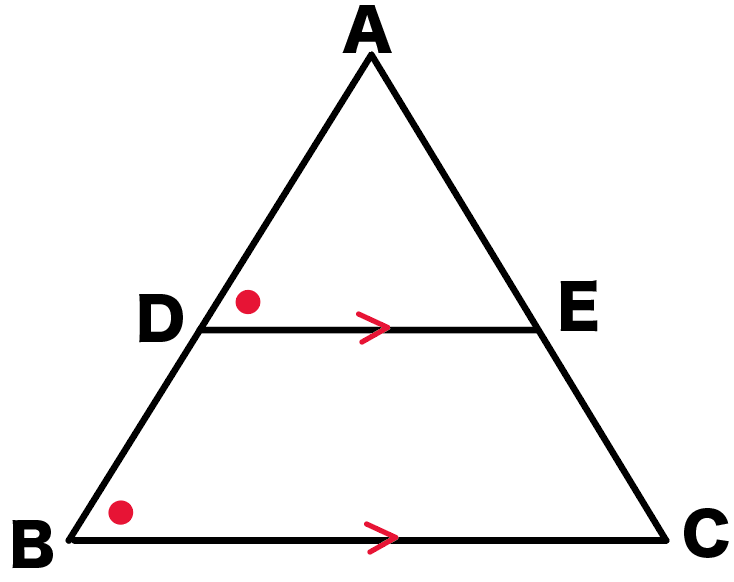



中3数学 中点連結定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
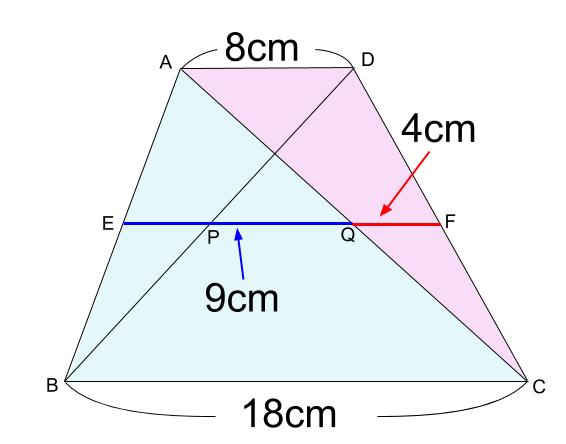



中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




数学 中3 49 平行線と線分の比 基本編 Youtube
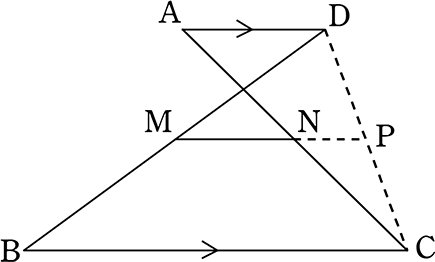



中学数学 図形の相似



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




中点連結定理を利用した証明 チーム エン




中点連結定理の問題です の問題が分からないので 教えてください お願いします Clear




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




中点連結定理の一証明 身勝手な主張



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
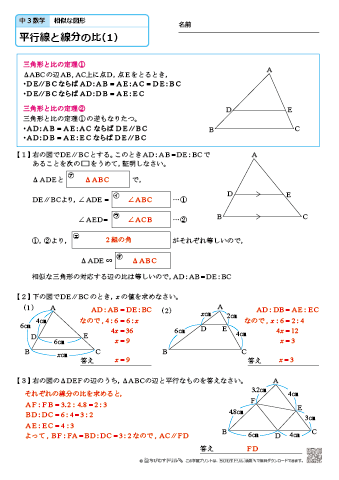



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
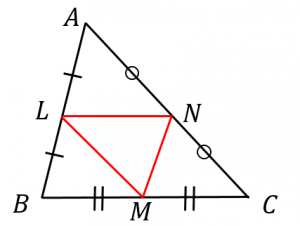



中点連結定理とその逆の証明および例題 具体例で学ぶ数学




中点連結定理の一証明 身勝手な主張




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行線と比の定理を利用した証明 Geogebra



中学数学 中点連結定理 中学数学の無料オンライン学習サイトchu Su
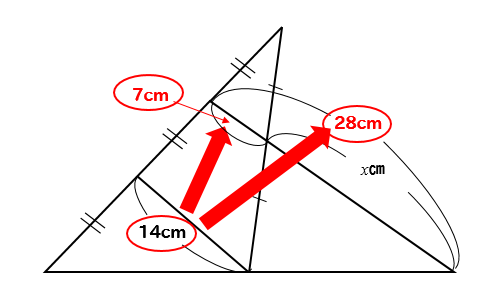



中3相似 中点連結定理 三等分の三角形求め方を問題解説 数スタ




三角形と比の定理の証明3 Geogebra



おもしろ数学講座
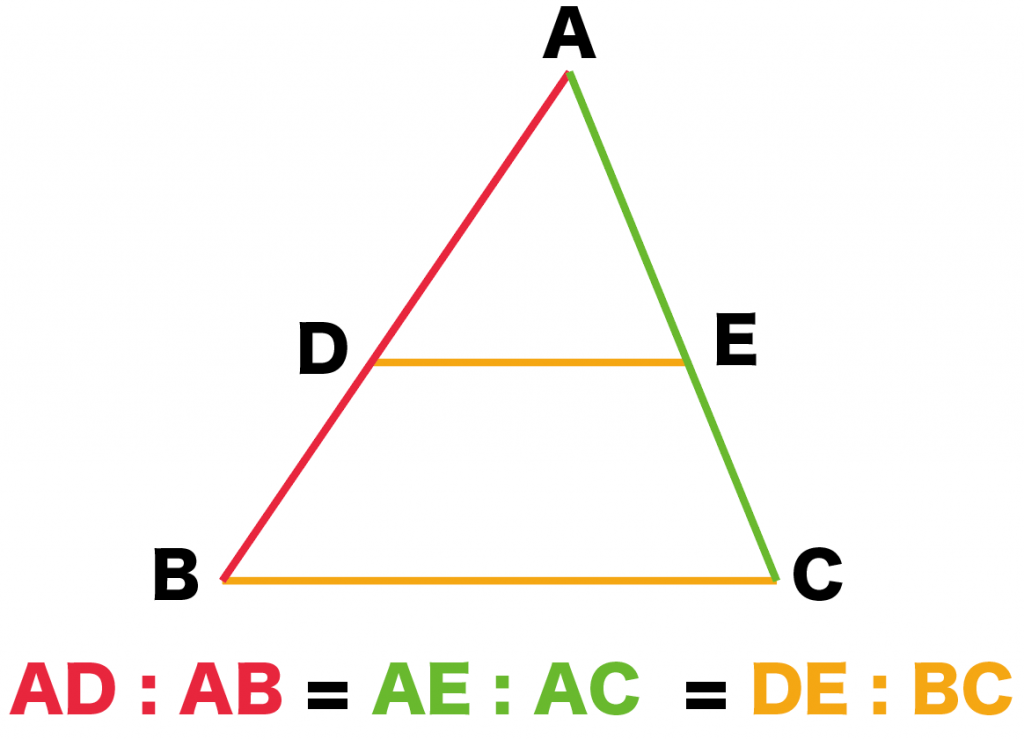



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく



1



中点連結定理とは 証明 定理の逆や応用 問題の解き方 受験辞典




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア



0 件のコメント:
コメントを投稿